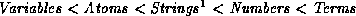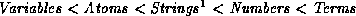Standard Order of Terms

Comparison and unification of arbitrary terms. Terms are ordered in the so called ``standard order''. This order is defined as follows:

1. 
2. 
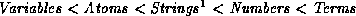
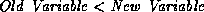
3. Atoms are compared alphabetically.
4. Strings are compared alphabetically.
5. Numbers are compared by value. Integers and floats are treated identically.
6. Terms are first checked on their functor (alphabetically), then on their arity and finally recursively on their arguments, leftmost argument first.

+Term1 == +Term2
  Succeeds if Term1 is equivalent to Term2. A variable is only identical to a sharing variable.

+Term1 \== +Term2
  Equivalent to ` Term1 == Term2'.

+Term1 = +Term2
  Unify Term1 with Term2. Succeeds if the unification succeeds.

+Term1 \= +Term2
  Equivalent to ` Term1 = Term2'.

+Term1 =@= +Term2
  Succeeds if Term1 is `structurally equal' to Term2. Structural equivalence is weaker than equivalence ( ==/2), but stronger than unification ( =/2). Two terms are structurally equal if their tree representation is identical and they have the same `pattern' of variables. Examples:

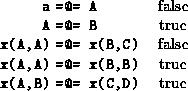
+Term1 \=@= +Term2
  Equivalent to `\+ Term1 =@= Term2'.

+Term1 @< +Term2
  Succeeds if Term1 is before Term2 in the standard order of terms.

+Term1 @=< +Term2
  Succeeds if both terms are equal ( ==) or Term1 is before Term2 in the standard order of terms.

+Term1 @> +Term2
  Succeeds if Term1 is after Term2 in the standard order of terms.

+Term1 @>= +Term2
  Succeeds if both terms are equal ( ==) or Term1 is after Term2 in the standard order of terms.