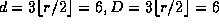 , og l = 3N = 192. Dermed blir
, og l = 3N = 192. Dermed blir 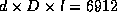 .
.
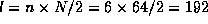 . Vi
har dermed
. Vi
har dermed 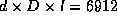 .
.
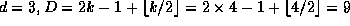 , og
, og 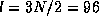 . Dermed blir
. Dermed blir 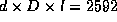 .
.
a)
For å konstruere et nettverk for en 64-node multidatamaskin, kan vi bruke:
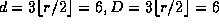 , og l = 3N = 192. Dermed blir
, og l = 3N = 192. Dermed blir 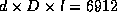 .
.
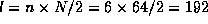 . Vi
har dermed
. Vi
har dermed 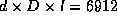 .
.
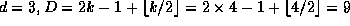 , og
, og 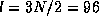 . Dermed blir
. Dermed blir 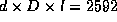 .
.
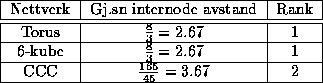
Resultatene er listet opp i tabellen under:
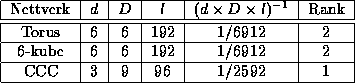
Hvis kvaliteten til et nettverk skal måles ved 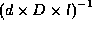 , er CCC-nettverket bedre enn 3D-torus og 6-kuben. En
3D-torus og 6-kube vil ha samme kvalitet.
, er CCC-nettverket bedre enn 3D-torus og 6-kuben. En
3D-torus og 6-kube vil ha samme kvalitet.
b)
3D-torus og hyperkuben har de samme nettverks-parametrene: Vi har
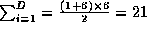 .
. 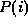 er
sannsynligheten for informasjonsutveksling mellom noder ved en avstand
i.
er
sannsynligheten for informasjonsutveksling mellom noder ved en avstand
i.
Vi har således:
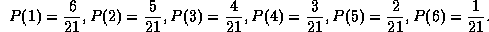
 blir da:
blir da:
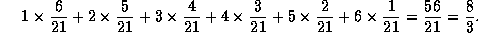
For CCC har vi 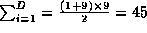 .
.
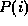 blir dermed:
blir dermed:
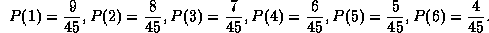
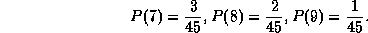
 blir her:
blir her:
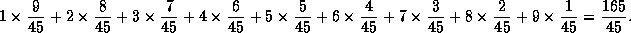
Konklusjonen her blir at  til 4-CCC nettverket er større en
det til 6-hyperkuben og 3D-torus. 6-hyperkuben og 3D-torus har samme
til 4-CCC nettverket er større en
det til 6-hyperkuben og 3D-torus. 6-hyperkuben og 3D-torus har samme
 -verdi. Likheten mellom 6-hyperkuben og 3D-torus er
slående: Faktisk har det blitt vist [Wang89] at når k = 4
(som her), vil en k-nær n-kube være eksakt tilsvarende en
2n-dimensjonell binær hyperkube.
-verdi. Likheten mellom 6-hyperkuben og 3D-torus er
slående: Faktisk har det blitt vist [Wang89] at når k = 4
(som her), vil en k-nær n-kube være eksakt tilsvarende en
2n-dimensjonell binær hyperkube.
a)
N innganger kan permuteres på; 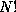 forskjellige måter.
forskjellige måter.
b)
Omega-nettet har n trinn, hver med 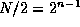 celler (svitsje-bokser); totalt har nettet altså;
celler (svitsje-bokser); totalt har nettet altså; 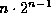 celler.
celler.
Siden det her kun er snakk om permutasjoner (ikke kringkasting), benyttes
to tilstander (parallell og kryss) i hver celle. Det samlede antall tilstander for nettet blir da 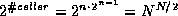 , og dette blir da antallet forskjellige permutasjoner som
kan utføres.
, og dette blir da antallet forskjellige permutasjoner som
kan utføres.
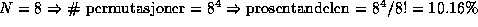 .
.
c)
Skriver
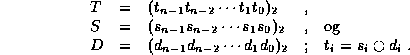
Rutingen foregår da slik: På; det i'te trinnet settes svitsje-cellen
til parallellforbindelse dersom  , og til kryssforbindelse
dersom
, og til kryssforbindelse
dersom  .
.
Fordeler ved å benytte T istedet for D er blant annet:
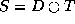
d)
Betrakt tilfellet at informasjon skal kringkastes fra PE , med
adresse
, med
adresse 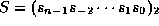 , til
, til 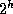 destinasjoner. Adressene til disse destinasjons-PE'ene avviker fra
hverandre i h bit, de resterende er like. La
destinasjoner. Adressene til disse destinasjons-PE'ene avviker fra
hverandre i h bit, de resterende er like. La 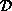 være mengden
av de h bitnummer (
være mengden
av de h bitnummer ( ) som angir hvilke bit som er
forskjellige i de h destinasjonsadressene. Rutingalgoritmen blir da,
for trinn i:
) som angir hvilke bit som er
forskjellige i de h destinasjonsadressene. Rutingalgoritmen blir da,
for trinn i:
if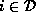
then
if
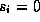
then
Kringkast fra den øvre inngangen til begge utganger
else
Kringkast fra den nedre inngangen til begge utganger
else
Følg regelen fra c) for denne cella