Bayesian Inference

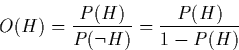
To infer knowledge from a Bayesian network, we use Bayesian inference. First we introduce some terminology:

Prior Odds are predictive support with only background knowledge:

$$O(H)=\frac{P(H)}{P(\neg H)} = \frac{P(H)}{1-P(H)}$$

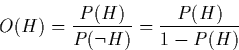
Likelihood Ratio is diagnostic support given to H by observed evidence:

$$L(e \mid H)=\frac{P(e \mid H)}{P(e \mid \neg H)}$$

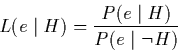
Posterior Odds are predictive support given observed evidence, e:

$$O(H \mid e)= \frac{P(H \mid e)}{P(\neg H \mid e)} = L(e \mid H) O(H)$$

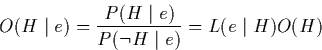
By using these definitions, we can infer knowledge like in probability theory. We illustrate this with an example:

A salesman has installed an alarm in a shop, and it is known that the alarm obeys these probabilities:

$$P(Alarm \mid Burglar) = 0.95$$

$$P(Alarm \mid \neg Burglar) = 0.01$$

P(Burgulary) = 10^-4

To find the probability that it is a burglar if the alarm goes, we do the following: First we find the posterior odds of it being a burglar:

$$O(Burglar \mid Alarm) = L(Alarm \mid Burglar) * O(Burglar) = \frac{0.95}{0.01 * 10^{-4}} = 0.0095$$

To convert odds to probability, we use: (deducted from the prior odds)

$$P(A) = \frac{O(A)}{1+O(A)}$$

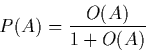
This implies:

$$P(Burglar \mid Alarm) = \frac{0.0095}{1+0.0095}=0.00941$$